Calcula el producto de convolución de dos señales.
Sintaxis
Convolution(Signal1, Signal2 [ , Mode = CONVOLUTION_NONCIRCULAR ])
La sintaxis de la función Convolution consta de los siguientes elementos:
Parte |
Descripción |
||||||
|---|---|---|---|---|---|---|---|
Signal1 |
La señal que se convoluciona con la segunda señal. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal y Serie de señales. Se permiten todos los tipos de datos numéricos. No se permiten valores inválidos en este argumento. Se aplican restricciones adicionales al componente X. Los valores deben tener un espaciado positivo constante. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||
Signal2 |
La señal que se convoluciona con la primera señal. Las estructuras de datos permitidas son Serie de datos, Matriz de datos, Señal y Serie de señales. Se permiten todos los tipos de datos numéricos. No se permiten valores inválidos en este argumento. Se aplican restricciones adicionales al componente X. Los valores deben tener un espaciado positivo constante. En los tipos de datos complejos se calcula un valor absoluto. Si el argumento es una lista, la función se ejecuta para cada elemento de la lista y el resultado también es una lista. |
||||||
Mode |
Especifica el modo de cálculo. El argumento Mode puede tener los siguientes valores:
Si el argumento es una lista, se toma su primer elemento. Si se trata de nuevo de una lista, se repite el proceso. Se establece el valor predeterminado CONVOLUTION_NONCIRCULAR si no se especifica el argumento. |
Notas
El resultado es siempre el tipo de datos En coma flotante de 64 bits.
La unidad del resultado es igual al producto de las unidades de Signal1 y Signal2.El producto de convolución para dos series de datos s y g se define como:
y N, el número de valores en s y g.
El cálculo se realiza en todos los casos en el dominio de la frecuencia según la fórmula siguiente:
IRFFTn(*FFTn(Signal1) * FFTn(Signal2))
Con argumentos bidimensionales, el cálculo se realiza columna por columna y el resultado también es bidimensional. Si uno de los argumentos tiene un componente X, esto también se aplica al resultado. El resultado contiene el desfase τ del producto de convolución. Nota: Si el otro argumento no tiene componente X, se asume para él el mismo muestreo que para el argumento con componente X.
Con la correlación cruzada circular, el cálculo se basa en la suposición de que uno o más períodos completos de las señales que se van a analizar están almacenados en Signal1 y Signal2. En este caso, los números de filas de Signal1 y Signal2 deben coincidir.
La convolución no circular se basa en el supuesto de que las señales fuera del rango definido por los conjuntos de datos Signal1 y Signal2 tienen un absoluto de cero. Antes de pasar al dominio de la frecuencia, se añade un número suficiente de ceros a los conjuntos de datos. El producto de convolución se calcula para todas las τ para las que puede tener un valor distinto de 0, es decir, para las que sigue habiendo solapamiento entre las dos señales.
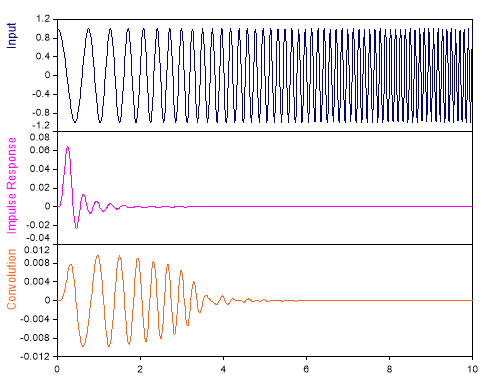
El siguiente gráfico muestra la convolución de una señal de coseno de frecuencia variable con la respuesta al impulso de un filtro de paso bajo para todo τ positivo:
Disponibilidad
FlexPro Basic, Professional, Developer Suite
Ejemplos
Dim Signal1 = Signal(0.5 * Square(2. * PI * 1.0 * (1000, 0.0, 0.001), 0.5) + 0.5, (1000, 0.0, 0.001))
Dim Signal2 = Signal(0.5 * Square(2. * PI * 1.0 * ((1000, 0.0, 0.001) + 0.5), 0.5) + 0.5, (1000, 0.0, 0.001))
Convolution(Signal1, Signal2, CONVOLUTION_NONCIRCULAR)
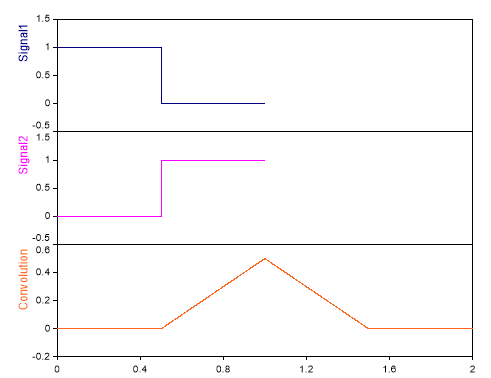
Producto de convolución no circular de dos señales rectangulares.
Véase también
Objeto de análisis Convolución
Bibliografía
[1] "Oppenheim, A. V. and Schafer, R. W.": "Discrete-Time Signal Processing, 2nd Edition", página 570 - 73. "Prentice Hall, New Jersey", 1999. ISBN 0-13-754920-2.
[2] "H. D. Lüke": "Signalübertragung", página 79 - 81. "Springer-Verlag Berlin, Heidelberg, New York", 1985. ISBN 3-540-15526-0.