Documentación de FlexPro 2025

LeastSquaresCircle

Calcula el círculo de mínimos cuadrados (LSCI) de un conjunto bidimensional de puntos (círculo de referencia de mínimos cuadrados). Se utiliza para determinar la redondez.

Sintaxis

LeastSquaresCircle(Points, [ OutputOptions = LSCI_OUTPUT_MIDDLE_CIRCLE ], [ CircleSize = 5000 ] [ , Algorithm = LSCI_ALGORITHM_KASA ])
o
LeastSquaresCircle(Y, X, [ OutputOptions = LSCI_OUTPUT_MIDDLE_CIRCLE ], [ CircleSize = 5000 ] [ , Algorithm = LSCI_ALGORITHM_KASA ])

La sintaxis de la función LeastSquaresCircle consta de los siguientes elementos:

Parte

Descripción

Points

El conjunto de puntos Y y X para los que debe calcularse el círculo de mínimos cuadrados. Ambos componentes de la señal deben tener la misma unidad.

Las estructuras de datos permitidas son Señal. Se permiten todos los tipos de datos reales excepto Tiempo de calendario y Intervalo de tiempo.

El conjunto de puntos Y utilizado para calcular el círculo de mínimos cuadrados. Si especifica una señal, se utiliza su componente Y. La unidad debe coincidir con la unidad del argumento X.

Las estructuras de datos permitidas son Serie de datos y Señal. Se permiten todos los tipos de datos reales excepto Tiempo de calendario y Intervalo de tiempo.

El conjunto de puntos X utilizado para calcular el círculo de mínimos cuadrados. Si especifica una señal, se utiliza su componente Y. La unidad debe coincidir con la unidad del argumento Y.

Las estructuras de datos permitidas son Serie de datos y Señal. Se permiten todos los tipos de datos reales excepto Tiempo de calendario y Intervalo de tiempo.

OutputOptions

Especifica qué resultados deben devolverse. Si hay varios resultados, se emiten en forma de lista. Si, por ejemplo, se desea obtener el radio del círculo de referencia y la redondez, el argumento debe tener el valor LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS + LSCI_OUTPUT_ROUNDNESS.

El argumento OutputOptions puede tener los siguientes valores:

Constante	Significado
+ LSCI_OUTPUT_ALL	Todas las salidas disponibles.
+ LSCI_OUTPUT_CENTER_X	Coordenada X del centro del círculo de referencia. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_CENTER_Y	Coordenada Y del centro del círculo de referencia. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_MIDDLE_CIRCLE	El círculo de referencia calculado (círculo de referencia de mínimos cuadrados). El resultado es una señal.
+ LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS	Radio del círculo de referencia. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_INSCRIBED_CIRCLE	El círculo interior más grande en relación con el círculo de referencia. El centro del círculo interior coincide con el centro del círculo de referencia. El radio del círculo interior es la distancia mínima entre el conjunto de puntos y el centro del círculo. El resultado es una señal.
+ LSCI_OUTPUT_INSCRIBED_CIRCLE_RADIUS	Radio del círculo interior en relación con el círculo de referencia. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_CIRCUMSCRIBED_CIRCLE	El círculo exterior más pequeño en relación con el círculo de referencia. El centro del círculo exterior coincide con el centro del círculo de referencia. El radio del círculo exterior es la distancia máxima entre el conjunto de puntos y el centro del círculo. El resultado es una señal.
+ LSCI_OUTPUT_CIRCUMSCRIBED_CIRCLE_RADIUS	Radio del círculo exterior en relación con el círculo de referencia. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_ROUNDNESS	Desviación de redondez. Es la diferencia entre los radios de los círculos exterior e interior. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_ROUNDNESS_MAX_TO_REF	Desviación de redondez de valor pico a valor de referencia. Es la diferencia entre LSCI_OUTPUT_CIRCUMSCRIBED_CIRCLE_RADIUS y LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_ROUNDNESS_REF_TO_MIN	Desviación de redondez de valor de referencia a valor valle. Es la diferencia entre LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS y LSCI_OUTPUT_INSCRIBED_CIRCLE_RADIUS. El resultado es un valor en coma flotante de 64 bits.
+ LSCI_OUTPUT_ROUNDNESS_QUADRATIC_MEAN	Media cuadrática de las desviaciones de los puntos de datos respecto al círculo de referencia. Corresponde a la raíz cuadrada de la media de los cuadrados de las desviaciones locales de redondez respecto al círculo de referencia de los cuadrados de desviación más pequeños. El resultado es un valor en coma flotante de 64 bits.

Se establece el valor predeterminado LSCI_OUTPUT_MIDDLE_CIRCLE si no se especifica el argumento.

CircleSize

Especifica el número de valores para presentar los círculos ajustados. Si introduce cero, se conserva el número de valores original. El argumento solo se tiene en cuenta si se ha seleccionado uno de los círculos de la lista para OutputOptions.

Las estructuras de datos permitidas son Valor escalar. Se permiten todos los tipos de datos enteros.

El valor debe ser mayor o igual que 0.

Se establece el valor predeterminado 5000 si no se especifica el argumento.

Algorithm

Determina el algoritmo de cálculo del círculo de mínimos cuadrados. Siempre se utiliza el método de mínimos cuadrados.

El argumento Algorithm puede tener los siguientes valores:

Constante

Significado

LSCI_ALGORITHM_KASA

Para calcular el círculo LSCI mediante el método de mínimos cuadrados, se utiliza la siguiente funcional modificada que hay que minimizar:Esto permite resolver explícitamente el ajuste de curva mediante un enfoque lineal de mínimos cuadrados. El procedimiento se conoce como método Kasa, véase [1], [2, capítulo 2] o [4]. El algoritmo es sencillo, rápido y robusto. Ofrece buenos resultados si los puntos de datos se muestrean a lo largo de todo un círculo o de una gran parte de él (al menos un semicírculo). Sin embargo, si los puntos de datos solo se muestrean a lo largo de un pequeño arco, el resultado se distorsiona y los círculos obtenidos suelen ser demasiado pequeños.

LSCI_ALGORITHM_PRATT

Para calcular el círculo LSCI mediante el método de mínimos cuadrados, se utiliza la siguiente funcional modificada que hay que minimizar:El procedimiento se conoce como método Pratt, véase [3] o [4]. El algoritmo es algo más lento que el método Kasa, pero preciso y sigue siendo rápido. En comparación con el método Kasa, se obtienen mejores resultados si los puntos de datos están dentro de un arco pequeño.

Se establece el valor predeterminado LSCI_ALGORITHM_KASA si no se especifica el argumento.

Notas

Los valores se convierten en números en coma flotante de 64 bits antes del cálculo.

Las opciones de salida del argumento OutputOptions se visualizan en el siguiente diagrama:

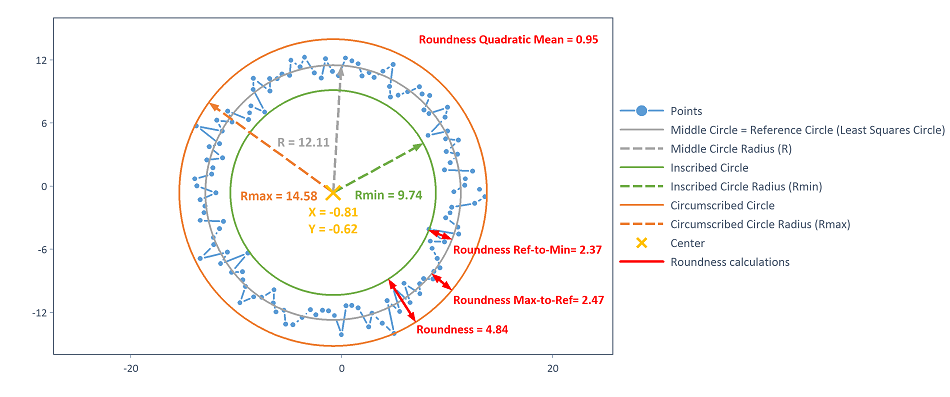
Se puede acceder a los resultados con los siguientes nombres de los elementos de lista:

Constante	Significado
.["Center_X"]	Coordenada X del centro del círculo de referencia.
.["Center_Y"]	Coordenada Y del centro del círculo de referencia.
.["Middle_Circle"]	Círculo de referencia (círculo de referencia de mínimos cuadrados).
.["Middle_Circle_Radius"]	Radio del círculo de referencia.
.["Inscribed_Circle"]	El círculo interior más grande en relación con el círculo de referencia.
.["Inscribed_Circle_Radius"]	Radio del círculo interior más grande en relación con el círculo de referencia.
.["Circumscribed_Circle"]	El círculo exterior más pequeño en relación con el círculo de referencia.
.["Circumscribed_Circle_Radius"]	Radio del círculo exterior más pequeño en relación con el círculo de referencia.
.["Roundness"]	Desviación de redondez como diferencia entre los radios de los círculos exterior e interior.
.["Roundness_Max_to_Ref"]	Desviación de redondez de valor pico a valor de referencia.
.["Roundness_Ref_to_Min"]	Desviación de redondez de valor de referencia a valor valle.
.["Roundness_Quadratic_Mean"]	Media cuadrática de las desviaciones de los puntos de datos respecto al círculo de referencia.

También puede utilizar siempre la sintaxis Formula.ListElementName.

Nota Los cálculos de redondez LSCI se basan en la norma actualmente vigente para la determinación de la redondez, véase [5].

Disponibilidad

FlexPro Professional, Developer Suite

Ejemplos

LeastSquaresCircle(y, x)

Calcula el círculo LSCI (círculo de referencia de mínimos cuadrados) de un conjunto de puntos.

LeastSquaresCircle(y, x, LSCI_OUTPUT_ROUNDNESS)

Calcula el círculo de mínimos cuadrados de un conjunto de puntos y devuelve solo la redondez.

LeastSquaresCircle(points, LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS + LSCI_OUTPUT_ROUNDNESS)

Calcula el círculo de mínimos cuadrados de un conjunto de puntos. Como resultado, se emiten el radio del círculo de referencia y la redondez en forma de lista.

Dim alpha = Series(0, 2*PI, 0.05)
Dim r = 11.5 + Noise(1 # NumberOfRows(alpha), NOISE_NORMAL)
Dim points = Signal(Noise(1) + r*Sin(alpha), Noise(1) + r*Cos(alpha))
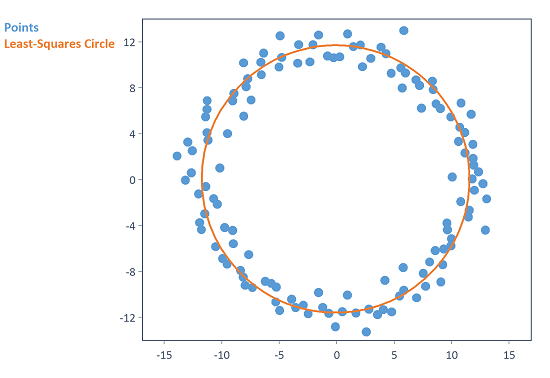
List("Points", points, "Least-Squares Circle", LeastSquaresCircle(points))

Calcula el círculo de mínimos cuadrados de puntos distribuidos aleatoriamente en el plano bidimensional.

Véase también

Función MaximumInscribedCircle

Función MinimumCircumscribedCircle

Función MinimumZoneCircle

Función GaussianFilter

Función NonLinCurveFit

Función Approximation

Objeto de análisis Aproximación circular

Bibliografía

[1] I. Kasa: A curve fitting procedure and its error analysis. En: IEEE Trans. Inst. Meas., Vol. 25, Pages 8-14. http://ieeexplore.ieee.org/document/6312298/, 1976.

[2] L.D. Coope: Circle fitting by linear and nonlinear least squares. En: Journal of Optimization Theory and Applications, Vol. 76, Issue 2, Pages 381-388. https://link.springer.com/article/10.1007/BF00939613, 1993.

[3] V. Pratt: Direct least-squares fitting of algebraic surfaces. En: Computer Graphics, Vol. 21, Pages 145-152. https://dl.acm.org/citation.cfm?id=37420, 1987.

[4] A. Al-Sharadqah and N. Chernov: Error Analysis for circle fitting algorithms. En: Electron. J. Statist., Vol. 3, Pages 886-911. https://projecteuclid.org/euclid.ejs/1251119958, 2009.

[5] DIN Deutsches Institut für Normung e.V.: Part 1: Vocabulary and parameters of roundness (ISO 12181-1:2011); English translation of DIN EN ISO 12181-1:2011. En: Geometrical product specifications (GPS)- Roundness. 2011.

Conozca, experimente y utilice FlexPro. ¡Asegure su excelencia personal en la evaluación de datos de medición!

Boletín Weisang

Asegure su excelencia personal en conocimiento y manténgase informado con nuestro boletín gratuito.

Pregunte a nuestros expertos

¿Quiere saber más sobre FlexPro y nuestros servicios personalizados? ¡Nuestros expertos están a su disposición!

Probar FlexPro gratis

Obtenga su versión de prueba gratuita y familiarícese con todas las funciones de FlexPro sin compromiso.