Calculates the Bessel function of the second kind with the order specified.
Syntax
Yn(n, Number)
The syntax of the Yn function consists of the following parts:
Part |
Description |
|---|---|
n |
The order. Permitted data structures are Scalar value. All integral data types are permitted. The value must be greater or equal to 0. |
Number |
The argument for the function. All data structures are allowed. All numeric data types are permitted. |
Remarks
The data type of the result is always 64-bit floating point.
The structure of the result corresponds to that of the argument Number. The calculation is done element-by-element where appropriate.
The result has the unit 1, if Number has a unit. Otherwise, it has no unit.
For composite data structures, only the Y component is calculated.
The real Bessel function is calculated for a real argument. The result then has the 64-bit floating point value data type. A void floating point value is output for values smaller than or equal to zero. The following illustration shows the course of the function for the orders 0 to 4 within the interval [0.01, 40]:
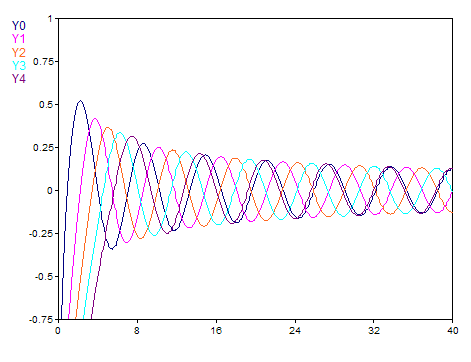
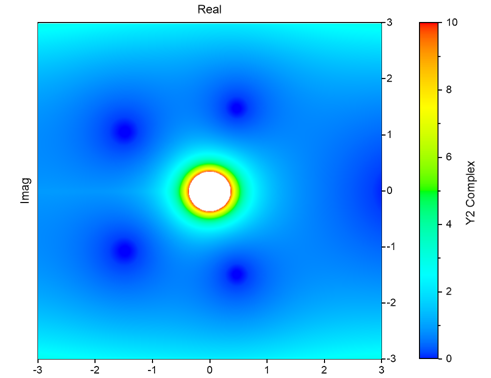
If Number is complex, the complex Bessel function is calculated. The result then has the complex 64-bit floating point value data type. The following graph shows the course of the absolute value of the function for order 2:
If the argument is a list, then the function is executed for each element of the list and the result is also a list.
Available in
FlexPro Basic, Professional, Developer Suite
Examples
Yn(2, 0) |
Results in ?. |
Dim x |
Calculates a list of three signals with the function curves of orders 0, 1 and 2 in the interval [0.1, 40]. |
See Also
References
[1] Donald E. Amos: AMOS - A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order. In: www.netlib.org. https://netlib.org/amos/, 1986.