Count Matrix Analysis Object (Counting Procedures Option)
You can use this analysis object to determine the Rainflow matrix or Markov (transition) matrix of a signal. You can then use the Rainflow Count Analysis Object to extract various univariate collectives, such as frequencies of peak values, from the matrices.
Matrix
The Markov matrix contains the absolute frequencies of all crossings in the load-time history. First, all turning points in the load-time history are determined. These turning points are then classed according to the class division. A pair of consecutive turning points is considered a transition. The class of the "from" point selects the row in the matrix and the "to" point class selects the column respectively. The crossing is counted in the resultant matrix position.
The frequencies of peak values, ranges and level crossings can be extracted form the Markov matrix. The Markov matrix does not sufficiently account for the requirements of the operational reliability test, since greater load alternations, in which smaller load alternations occur, are split up into a sequence of small transitions.
The Rainflow algorithmavoids this problem. Instead of the transitions between consecutive turning points, closed hystereses (range pairs)are counted here. These range pairs are load reversals, which at least return to their starting points. In the case of a large load cycle that includes smaller load reversals, these are first counted as small hystereses and then the large load cycle is counted as a large hysteresis. The hystereses are also described as range pairs. The following illustration shows how a range pair is taken from the curve without losing the large load cycle:
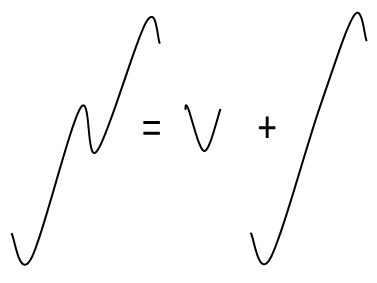
The above illustration also shows that this type of range pair consists of an ascending and descending transition of equal size. This type of range pair is therefore counted twice. This type of range pair is therefore counted twice in the "from"-"to" format of the Rainflow matrix: once as ascending and once as descending. Alternatively, the asymmetric format of the matrix can also be formed. In this case, only the first transition of the range pair is counted, which can be ascending or descending. This matrix format differentiates between "positive" and "negative" range pairs. The asymmetric matrix count total is only half as large as that of the symmetric matrix count total. The symmetric matrix can be derived from the symmetric matrix by adding the asymmetric matrix with its transposed values.
The result of the count is a signal series with a Z component. Its Y component contains the matrix with counted values, the X component contains the mid-points of the "from" classes, and the Z component contains those of the "to" classes. You can also output the Rainflow matrix in the range-mean format. In this case, the X component contains the lower limits of the range classes. All hystereses with the same absolute distance between "from" and "to" fall into a certain range class. The Z component contains the mid-points of the mean value classes. All hystereses with the same mean value from "from" and "to" fall into a certain mean value class. In this case as well, the closed hystereses are only counted once.
Residue
The disadvantage of the Rainflow procedure is that not all turning points satisfy the Rainflow algorithm. A so-called Residue often remains. The residue is generally a zigzag curve with ascending and descending amplitudes. You can exclude the residue from the matrix, include only a closed hysteresis "a-b-a" in the center of the residue in the matrix, or fully include the residue in the matrix. The residue should be included in the matrix, especially when univariate collectives, such as, for instance, peak values, are to be extracted from the Rainflow matrix. There are several procedures for this. The procedure described here in [1] is especially ideal. The residue in this case is divided at its highest point and the two halves are appended to each other in reverse order. This sequence then satisfies the algorithm and is included in the matrix. Alternatively, you can include the half cycles of the residue in the matrix, each with the count value 0.5, i.e. this assumes half the damage amount of a full hysteresis per half cycle of the residue [2].
Class division
The counting is based on the division of the value range of the load-time function (source data set) into discrete classes. Various procedures are available to help you create this division. Essentially, the location of the class limits is specified in all of the procedures. The procedures differ only in the choice of parameters that you have to specify in order to set the class limits. The classes are formed as open-top intervals from the class limits specified, i.e. the lower limit is included in the class in each case. An exception is the top class, which also includes the upper limit. Any values that lie above the top class or below the bottom class are not counted!
Selecting a suitable class division must be carefully planned, since only results that have been determined using the same class division can be directly compared. Load reversals in the load-time history that are smaller than the class width are only counted if they lie on a class limit. The location of the class limits thus affects the result of the count.
Hysteresis
You can use a hysteresis (range filter) to suppress smaller ranges or range pairs to reduce this effect. The hysteresis is a quantity independent of the position of the class limits. Only the ranges or range pairs whose amplitudes at least correspond to the hysteresis are used. The hysteresis is specified as a percentage of the class width, or in the case of non-equidistant class divisions, as the average class width.
References
[1] de Jonge, J.B. (1980). Counting Methods for the Analysis of Load Time Histories. NLR Memorandum SB-80-106 U
[2] ASTM E1049-85(2017). Standard Practices for Cycle Counting in Fatigue Analysis. STM International, West Conshohocken, PA, 2017
