PolynomialInterpolation (FPScript)
Führt eine Polynominterpolation an vorgebbaren Stützstellen aus. Unter Polynominterpolation versteht man die Suche nach einem Polynom, das exakt durch die vorgegebenen Punkte verläuft.
Syntax
PolynomialInterpolation(DataSet)
oder
PolynomialInterpolation(DataSet, X)
oder
PolynomialInterpolation(DataSet, N, SamplingMode)
Die Syntax der PolynomialInterpolation-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||
|---|---|---|---|---|---|---|---|
DataSet |
Gibt die Stützstellen an, für die die Interpolation durchgeführt werden sollen. Wenn Sie eine Datenreihe angeben, wird die X-Komponente automatisch generiert. Das berechnete Polynom geht exakt durch alle Stützstellen. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal und Signalreihe. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
X |
Gibt einen Datensatz mit den X-Werten an, für die das Polynom ausgewertet wird. Erlaubte Datenstrukturen sind Einzelwert und Datenreihe. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
N |
Gibt die Anzahl der Punkte insgesamt bzw. pro X-Intervall des Signals an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
SamplingMode |
Gibt an, wie das berechnete Polynom abgetastet werden soll. Das Argument SamplingMode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Wird die Funktion nur mit dem Argument DataSet aufgerufen, so liefert die Funktion die Polynomialkoeffizienten zurück. In den beiden anderen Fällen wird das interpolierte Signal zurückgegeben. Bei n Stützstellen wird ein Polynom vom Grad n - 1 ermittelt. Die Polynominterpolation ist auch unter dem Begriff Lagrange-Interpolation bekannt. Für die Berechnung wird der Neville-Algorithmus verwendet.
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
Dim x = Series(-5,5,1)
Dim runge = Signal(1. / (1 + x ^ 2), x)
PolynomialInterpolation(runge, Series(runge.x[0], runge.x[-1], 0.1))
Führt eine Polynominterpolation der Runge-Funktion (n=11) mit einer Abtastrate 0,1 durch.
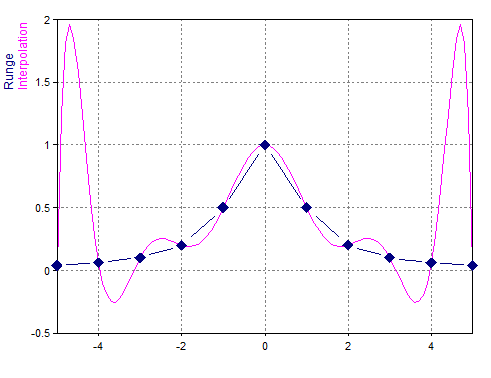
PolynomialInterpolation(runge, 100, POLYNOMIALINTERPOLATION_EQUIDISTANT)
Führt eine Polynominterpolation der Runge-Funktion (n=11) mit 100 äqudistant abgetasteten Werten durch.
PolynomialInterpolation(runge)
Liefert die Koeffizienten der Polynominterpolation der Runge-Funktion (n=11) zurück.
Siehe auch
Analyseobjekt Spline-Interpolation
Analyseobjekt Oberflächeninterpolation
Literatur
[1] "William H. Press et al.": "Numerical Recipes in C, Second Edition", Seite 108-122. "Cambridge University Press",1992.ISBN 0-552-43108-5.
