Integral (FPScript)
Berechnet das Integral.
Syntax
Integral(Signal [ , Mode = INTEGRAL_TRAPEZOIDAL ])
oder
Integral(Amplitude, Time [ , Mode = INTEGRAL_TRAPEZOIDAL ])
Die Syntax der Integral-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||
|---|---|---|---|---|---|---|---|---|---|
Signal |
Das Signal, dessen Integral berechnet wird. Wenn das Argument eine Datenreihe oder eine Datenmatrix ist, wird Eins als Schrittweite dX für die Integration angenommen. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||
Amplitude |
Die Y-Komponente des zu integrierenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||
Time |
Die X-Komponente des zu integrierenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||
Mode |
Zur diskreten Berechnung des Integrals werden Approximationsformeln verschiedener Genauigkeitsordnungen verwendet. Das Argument Mode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert INTEGRAL_TRAPEZOIDAL gesetzt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Die Einheit des Ergebnisses ist gleich dem Produkt der Einheiten der Y- und X-Komponente von Signal. Die Werte werden vor der Berechnung in 64-Fließkommazahlen gewandelt. Bei Datenmatrizen und Signalreihen erfolgt die Berechnung spaltenweise. Die X- bzw. Z-Komponenten werden, falls vorhanden, unverändert in das Ergebnis übernommen. Das Ergebnis kann als Stammfunktion des Signals betrachtet werden.
Das Integral wird im Modus INTEGRAL_TRAPEZOIDAL mit Hilfe der Trapezformel berechnet (mindestens zwei Datenpunkte vorausgesetzt):
Die Trapezregel kann auch auf nicht-äquidistante abgetastete Datensätze angewendet werden.
Im Modus INTEGRAL_SIMPSON wird das Integral mit Hilfe der Simpsonregel berechnet. Die Simpsonregel benötigt äquidistant abgetastete Datensätze (mindestens drei Datenpunkte vorausgesetzt):
Im Modus INTEGRAL_CUBIC wird das Integral mit Hilfe einer kubischen Integrationsformel berechnet. Diese Integrationsregel ist die zentralisierte Form der Adam's Integrationsregel (Adams interpolation formula oder auch Ngo integrator, siehe [4]. Die Regel benötigt ebenso äquidistant abgetastete Datensätze (mindestens vier Datenpunkte vorausgesetzt):
In allen Modi ist das Integral am linken Rand I[0] als 0 definiert. Für die Simpsonregel sowie die kubische Integrationsregel stehen an den Rändern I[1] sowie im kubischen Fall für den rechten Rand I[N] nicht genügend Stützstellen für die Approximationsformel zur Verfügung. An diesen Stellen werden Berechnungsvorschriften verwendet, die die gleiche Genauigkeitsordnung besitzen (analog zu [2, Seite 98]).
Hinweis Generell gilt: Je höher die Genauigkeitsordnung bei Wahl der Integrationsregel, desto größer ist die Genauigkeit bei Bestimmung des Integrals für glatte (nicht-verrauschte) Datensätze. Sind die Datensätze hingegen verrauscht, so wird der numerische Fehler bei Bestimmung des Integrals vergrößert, wenn eine Integrationsregel höherer Ordnung verwendet wird. Die Wahl des Integrationsmodus sollte also von dem Rauschen / der Glätte des zugrundeliegenden Datensatzes abhängig gemacht werden.
Ist man hingegen am Frequenz-Spektrum interessiert, so hilft es die Integrationsregeln als digitale Filter (siehe auch [1] oder [3, Sektion 7.2]) zu betrachten. Die Integrationsregeln besitzen hierbei den folgenden Amplitudengang. Aufgezeichnet ist ebenso der ideale Integrator (Filterverlauf der kontinuierlichen Integration):
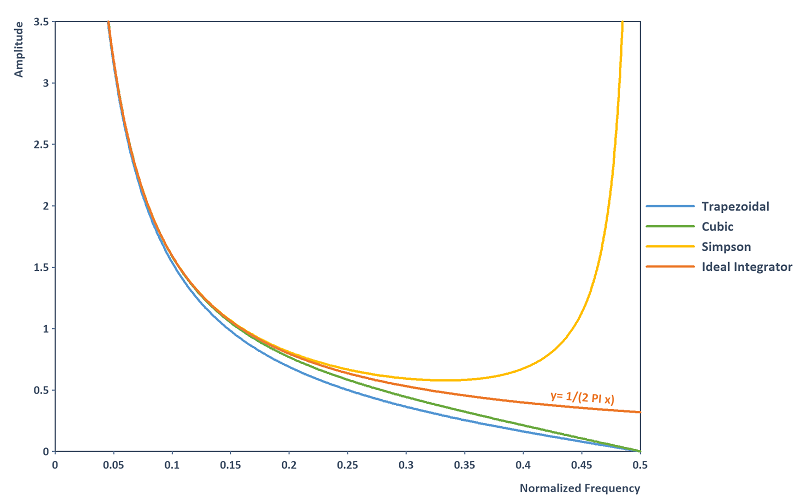
Beobachtung: Die Trapezregel sowie die kubische Integrationsregel besitzen durch Unterbewertung des idealen Integrators eine natürliche Tiefpass-Charakteristik und unterdrücken hochfrequentes Rauschen. Die kubische Integrationsregel besitzt dabei im gesamten Frequenzbereich eine präzisere Amplitudengang-Approximation des idealen Integrators als die Trapezregel. Die Simpsonregel besitzt im Frequenzbereich bis ca. 0,25 die exakteste Amplitudengang-Approximation des idealen Integrators, divergiert aber im Bereich der Nyquist-Grenze 0,5. Hochfrequentes Rauschen wird durch die Simpson-Regel daher verstärkt. Es sei angemerkt, dass alle Approximationsregeln einen konstanten Phasengang von -90 Grad besitzen und somit mit dem Phasengang des idealen Integrators übereinstimmen.
Verfügbarkeit
FlexPro View, Basic, Professional, Developer Suite
Beispiele
Integral({1,2,3,2,1}, {0,1,2,3,4})
Berechnet das Integral {0, 1.5, 4, 6.5, 8} der als Argument angegebenen Datenreihe mit Hilfe der Trapezregel.
Integral(Signal)[-1]
Berechnet die Fläche unter dem Kurvenverlauf eines Signals. Dazu muss der letzte Wert aus dem Ergebnis entnommen werden.
Integral(Detrend(Signal))
Integriert ein periodisches Signal und entfernt vorher den Mittelwert. Hier wurde die Detrend-Funktion verwendet, um den Gleichanteil oder einen linearen bzw. adaptiven Trend aus dem Signal vor der Integration zu entfernen. Begründung: Wenn Sie periodische Signale integrieren, die einen Mittelwert ungleich Null haben, dann läuft die integrierte Kurve durch Akkumulation des Mittelwerts im Signal weg. Folgende Grafik verdeutlicht den Sachverhalt:
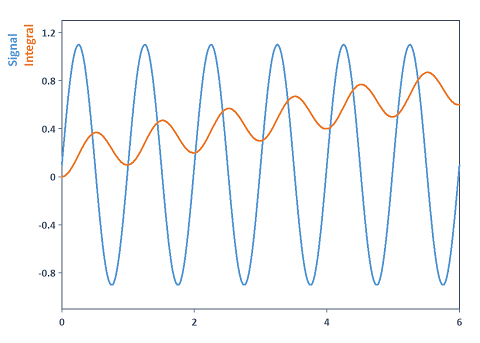
Integral(DCRemovalFilter(Signal))
Integriert ein Signal und entfernt vorher den Drift bzw. Gleichanteil. Zur Entfernung des Drifts bzw. Gleichanteils wurde nun die DCRemovalFilter-Funktion anstelle der Detrend-Funktion verwendet. Begründung: Ursache für das Wegdriften des Signals nach der Integration ist nicht nur die Akkumulation des Gleichanteils während der Integration, sondern auch der zur Frequenz umgekehrt proportionale Amplitudengang des Integrators. Durch diesen wird Rauschen bei Frequenzen nahe des Gleichanteils verstärkt und durch die Integration auf beliebig große Werte angehoben. Die integrierte Kurve läuft dann weg. Um das Wegdriften zu verhindern genügt es nicht den Mittelwert zu subtrahieren, sondern es müssen ebenso Frequenzanteile nahe des Gleichanteils mittels einem Hochpassfilter abgeschnitten werden. Folgende Grafik verdeutlicht diesen Sachverhalt (exemplarisch wurde zur Integration eines der Beschleunigungssignale aus den FlexPro-Beispieldaten unter C:\Users\Public\Documents\Weisang\FlexPro verwendet):
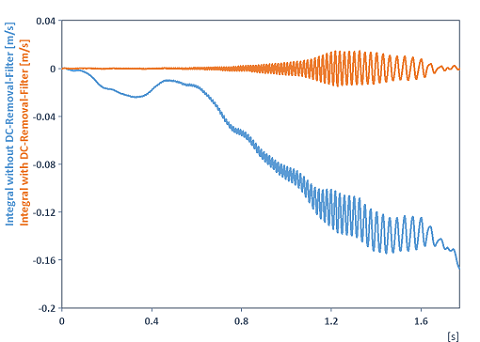
Dim filterCoef = List("b", {1/3, 4/3, 1/3}, "a", {1, 0, -1})
AmplitudeResponse(filterCoef)
Berechnet den Amplitudengang des Simpson-Filters mittels der AmplitudeResponse-Funktion.
Dim x = Series(0, 6, 0.5)
Integral(Signal(2.2 + 6.2*x + 12.6*x^2 - 2*x^3, x), INTEGRAL_CUBIC)
Berechnet das Integral eines Polynoms dritten Grades an den Stützstellen x. Das Ergebnis stimmt mit dem exakten Integral Signal(2.2*x + 3.1*x^2 + 4.2*x^3 - 0.5*x^4, x) überein.
Dim x = (30, 1, 0.1)
Dim f = Signal(50 * 1/x, x)
Dim integralExact = Signal(50 * log(x), x)
Absolute(Integral(f, INTEGRAL_TRAPEZOIDAL)[-1] - integralExact[-1])
Ermittelt für den Modus INTEGRAL_TRAPEZOIDAL den Fehler bei Berechnung des numerischen Integrals der glatten Funktion f = 50 * 1/x. Der Fehler ist proportional zu 0.01. Wählt man hingegen INTEGRAL_SIMPSON, so liefert dies ein Fehler proportional zu 0.001. Wählt man INTEGRAL_CUBIC, so liefert dies die höchste Genauigkeit mit einem Fehler proportional zu 0.0001.
Siehe auch
SavitzkyGolayDerivative-Funktion
Literatur
[1] Tilman Butz: Fourier Transformation for Pedestrians. Springer Berlin Heidelberg New York,http://www.springer.com/de/book/9783319169842,2015.ISBN 3-540-23165-X.
[2] C. Woodford, C. Phillips: Numerical Methods with Worked Examples. Chapman and Hall, 2-6 Boundary Row, London SE1 8HN, UK,1997.ISBN 0-412-72150-3.
[3] Richard G. Lyons: Understanding Digital Signal Processing (3rd Edition). Prentice Hall,2011.ISBN 0-13-702741-9.
[4] N. Q. Ngo: A new approach for the design of wideband digital integrator and differentiator. In: IEEE Trans. Circuits Syst. II, Exp. Briefs, Vol. 53, No. 9, Pages 936-940. Prentice Hall,2006.
