FIRFilterEquiripple (FPScript)
Berechnet die Impulsantwort eines FIR-Bandfilters mithilfe des Equiripple-Algorithmus.
Syntax
FIRFilterEquiripple(NumberOfBands, BandEdges, GainFactor, WeightingOfErrors, [ FilterLength ] [ , SamplingRate ])
Die Syntax der FIRFilterEquiripple-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
|---|---|
NumberOfBands |
Gibt die Anzahl der Bänder an. Die Anzahl der Bänder muss zwischen 1 und 40 liegen. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 und kleiner gleich 40 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
BandEdges |
Gibt die unteren und oberen Bandgrenzen an. Die Frequenzen liegen zwischen 0 und der halben Abtastrate bzw. bei normierten Frequenzen zwischen 0 und 0,5. Erlaubte Datenstrukturen sind Datenmatrix. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
GainFactor |
Gibt die Amplituden der Bänder an. 1 definiert einen Bandpass und 0 definiert eine Bandsperre. Erlaubte Datenstrukturen sind Datenmatrix und Signal. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
WeightingOfErrors |
Eine Datenreihe oder ein Signal mit der Gewichtung der Fehler, wenn die Filterlänge angegeben wird bzw. eine Datenreihe mit den maximalen Approximationsfehlern für die einzelnen Bänder. Erlaubte Datenstrukturen sind Datenreihe und Signal. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Für die X-Komponente gelten zusätzliche Beschränkungen.Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
FilterLength |
Gibt die Filterlänge an. Das Argument ist optional. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer 4 und kleiner 1000 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
SamplingRate |
Gibt die Abtastrate an. Das Argument ist optional. Wenn eine Abtastrate angegeben wird, so werden für die Grenzfrequenzen statt der normierten Frequenzen die absoluten Grenzfrequenzen angegeben. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Der Wert muss größer 0 sein. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
Anmerkungen
Die Koeffizienten des Filters werden als Datenreihe zurückgegeben. Verwenden Sie die Funktion Filter, um Daten mit den berechneten Filterkoeffizienten zu filtern.
Das Argument BandEdges ist eine Datenmatrix mit n Datenreihen mit je zwei 64-Bit Fließkommazahlen, wobei n die Anzahl der Bänder ist. Der erste Wert einer Datenreihe gibt die untere Bandgrenze an und der 2. Wert die obere Bandgrenze. Die Werte müssen aufsteigend sortiert sein und die Breite des Übergangs zwischen zwei Bändern muss größer als 0 sein.
Das Argument GainFactor kann eine Datenmatrix mit n (n = Anzahl der Bänder) Datenreihen mit je zwei 64-Bit Fließkommazahlen oder ein Signal sein. 1 definiert einen Bandpass und 0 definiert eine Bandsperre. Ist der Verstärkungsfaktor eine Matrix, so werden die Werte den Bandgrenzen zugeordnet. Daraus wird der Amplitudengang der Bänder ermittelt. Wird ein Signal angegeben, so lässt sich ein beliebiger Amplitudengang angeben. Die Y-Komponente enthält die Amplitude und die X-Werte die dazugehörigen Frequenzen von 0 bis zur halben Abtastrate bzw. von 0 bis 0,5. Dabei werden allerdings nur die Frequenzbereiche verwendet, die in der Liste mit den Frequenzbändern definiert sind.
Das Argument WeightingOfErrors kann eine Datenreihe mit n 64-Bit Fließkommazahlen oder ein Signal sein. Wird die Filterlänge angegeben, so lassen sich an dieser Stelle die Gewichtung der Fehler angeben, d.h. das Verhältnis der Fehlergrenzen der einzelnen Bänder zueinander. Wird keine Filterlänge angegeben, so werden die absoluten Fehlergrenzen für die einzelnen Bänder angeben und daraus die optimale Filterlänge ermittelt. Eine höhere Gewichtung eines Frequenzbandes gegenüber einem anderen bedeutet eine niedrigere Fehlergrenze, d.h. eine geringere Welligkeit. Bei angegebener Filterlänge lässt sich die Gewichtung auch als Signal angeben, wobei die X-Komponente die Frequenzen von 0 bis zur halben Abtastrate bzw. von 0 bis 0,5 enthält. Wird sowohl der Verstärkungsfaktor als auch die Gewichtung als Signal angegeben, so müssen beide Signale die gleichen X-Werte enthalten.
Hinweis Eine Erhöhung der Ordnung / Filterlänge bewirkt eine Vergrößerung der Steilheit des Filters und eine Verringerung der Welligkeit.
Verfügbarkeit
Option Digitale Filter
Beispiele
FIRFilterEquiripple(3, {{0, 0.1},{0.12, 0.2},{0.22, 0.5}}, {{0, 0},{1, 1},{0, 0}}, {0.05, 0.01, 0.1})
Folgende Grafik zeigt den Frequenzgang des berechneten Multiband-FIR-Filters. Es handelt sich dabei um drei Bänder (Sperrbereich, Durchlassbereich, Sperrbereich) mit Frequenzbereichen 0 bis 0,1, 0,12 bis 0,2 und 0,22 bis 0,5. Der maximale Fehler des ersten Bandes ist 0,05, der Fehler des zweiten Bandes ist 0,01 und der Fehler des dritten Bandes ist 0,1.
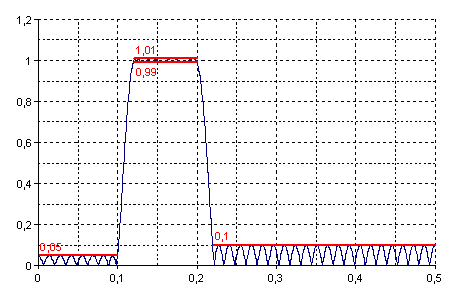
Anhand der vorgegebenen Spezifikation ermittelt die Funktion einen FIR-Filter der Länge 77 mit folgender Impulsantwort:
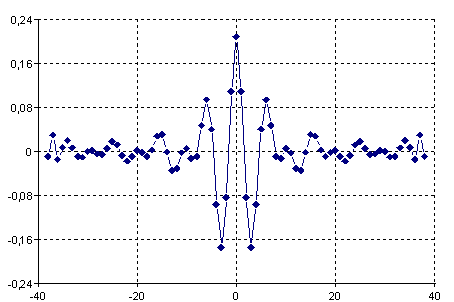
Folgende Grafik zeigt einen Wobbelsinus, der mit dem entworfenen Filter gefiltert wurde:
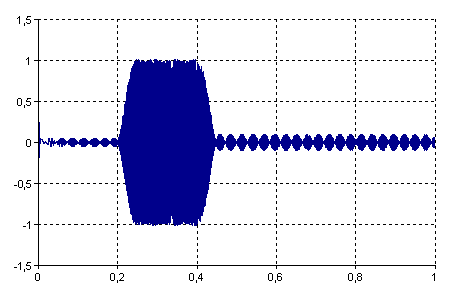
Filter(Signal, FIRFilterEquiripple(3, {{0 Hz, 100 Hz},{120 Hz, 200 Hz},{220 Hz, 500 Hz}}, {{0, 0},{1, 1},{0, 0}}, {0.05, 0.01, 0.1}, , SamplingRate(Signal)), , TRUE)
Die Funktion filtert ein Signal mit Phasenkorrektur mit dem im ersten Beispiel berechneten Filter. Bitte beachten Sie, dass das zweite Argument der Funktion Filter leer gelassen wird.
