Analyseobjekt Korrelation *
Mit diesem Analyseobjekt können Sie entweder die Autokorrelationsfunktion eines Datensatzes oder die Kreuzkorrelationsfunktion zweier Datensätze berechnen. Die Kreuzkorrelation beschreibt die Ähnlichkeit zweier Signale. Die Autokorrelation beschreibt die Ähnlichkeit eines Signals mit sich selbst.
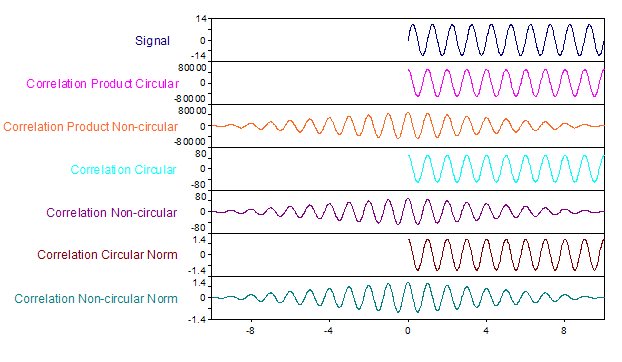
Bei der zirkulären Korrelation erfolgt die Berechnung unter der Annahme, dass im Datensatz bzw. in beiden Datensätzen eine oder mehrere vollständige Perioden eines periodischen Signals abgelegt sind. Bei der Kreuzkorrelation müssen beide Datensätze gleiche Werteanzahl haben. Diese Werteanzahl hat dann auch das Ergebnis. Hat das Ergebnis eine X-Komponente, so enthält dieses den Zeitversatz τ der Korrelationsfunktion. Bei der Autokorrelation befindet sich der Wert τ = 0 immer am Anfang der X-Datenreihe. Es werden also hier keine negativen τ berechnet. Wegen der Periodizität der Autokorrelation können in diesem Fall die Werte in der zweiten Hälfte des Ergebnisses jedoch auch als negative τ aufgefasst werden.
Die nicht-zirkuläre Korrelation basiert auf der Annahme, dass das Signal bzw. beide Signale außerhalb des durch die Datensätze gegebenen Ausschnitts den Betrag Null haben. Vor dem Übergang in den Frequenzbereich wird deshalb eine ausreichende Anzahl von Nullen an den Datensatz bzw. an beide Datensätze angehängt. Falls das Ergebnis eine X-Komponente hat, dann enthält diese den Zeitversatz τ der Korrelationsfunktion. Bei der Autokorrelation befindet sich der Wert τ = 0 immer genau in der Mitte der X-Datenreihe.
Die Werte der normierten Korrelation liegen zwischen -1 und +1.
Folgende Grafik zeigt die verschiedenen Varianten der Autokorrelationsfunktion für ein Sinussignal mit Frequenz 1, Amplitude 10 und einem X-Bereich von 0 bis 10:
Verwendete FPScript-Funktionen
Siehe auch
* Dieses Analyseobjekt ist in FlexPro View nicht verfügbar.
