Analyseobjekt Faltung *
Mit diesem Analyseobjekt können Sie das Faltungsprodukt zweier Datensätze berechnen.
Beim zirkulären Faltungsprodukt erfolgt die Berechnung unter der Annahme, dass in beiden Datensätzen eine oder mehrere vollständige Perioden eines periodischen Signals abgelegt sind. Für diese Variante müssen beide Datensätze gleiche Werteanzahl haben. Diese Werteanzahl hat dann auch das Ergebnis. Hat eines der Argumente eine X-Komponente, so gilt dies auch für das Ergebnis. Das Ergebnis enthält dann den Zeitversatz τ der Faltung.
Das nicht-zirkuläre Faltungsprodukt basiert auf der Annahme, dass die Signale außerhalb des durch die Datensätze gegebenen Ausschnitts den Betrag Null haben. Vor dem Übergang in den Frequenzbereich wird deshalb eine ausreichende Anzahl von Nullen an beide Datensätze angehängt. Hat eines der Argumente eine X-Komponente, so gilt dies auch für das Ergebnis. Das Ergebnis enthält dann den Zeitversatz τ der Faltung. Das Faltungsprodukt wird für alle τ berechnet, für die dieses einen Wert ungleich 0 haben kann, d. h. für die noch eine Überlappung der beiden Signale vorliegt.
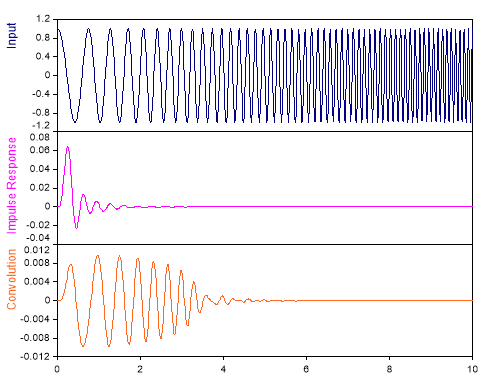
Die folgende Abbildung zeigt eine Anwendung des Faltungsintegrals. Es handelt sich hierbei um eine Tiefpassfilterung im Zeitbereich. Das Signal wird mit der Impulsantwort eines Tiefpassfilters gefaltet:
Verwendete FPScript-Funktionen
Siehe auch
* Dieses Analyseobjekt ist in FlexPro View nicht verfügbar.
