CompensatingSpline (FPScript)
Interpoliert einen Datensatz durch eine ausgleichende Spline-Kurve und tastet diese an vorgebbaren Stellen ab.
Syntax
CompensatingSpline(DataSet, N, SamplingMode, Weighting)
oder
CompensatingSpline(Amplitude, Time, N, SamplingMode, Weighting)
Die Syntax der CompensatingSpline-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||
|---|---|---|---|---|---|---|---|
DataSet |
Der Datensatz mit konstantem Abtastintervall, welcher interpoliert wird. Wenn Sie eine Datenreihe angeben, wird die X-Komponente automatisch generiert. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
Amplitude |
Die Y-Komponente des zu interpolierenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
Time |
Die X-Komponente des zu interpolierenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
N |
Gibt die Anzahl der Punkte insgesamt bzw. pro X-Intervall des Signals an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
SamplingMode |
Gibt an, wie die berechnete Spline-Kurve abgetastet werden soll. Das Argument SamplingMode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
Weighting |
Gibt das Maß des Ausgleichs für die Spline-Kurve an. Werte nahe Null ergeben eine Bestgerade, sehr große Werte eine natürliche Spline-Kurve. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt. Der Wert muss größer 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Das Ergebnis hat die gleiche Einheit wie das Argument DataSet.
Eine Spline-Kurve besteht aus kubischen Polynomen, die so aneinander gehängt werden, dass ein möglichst glatter Verlauf entsteht. Die Polynome gehen bei der approximierenden Spline-Funktion nicht zwingend durch die Punkte des Datensatzes, sondern gleichen diese aus. Das Maß des Ausgleichens kann von der natürlichen Spline-Funktion, die durch die Punkte geht, bis zur bestapproximierenden Geraden variiert werden. Die Y-Komponente des zu interpolierenden Datensatzes muss mindestens 3 Werte enthalten und die X-Komponente muss streng monoton wachsend sein. Vor der Spline-Interpolation werden ungültige Werte in der Y-Komponente durch lineare Interpolation eliminiert.
Die folgende Grafik zeigt ausgleichende Spline-Kurven mit unterschiedlichen Wichtungen:
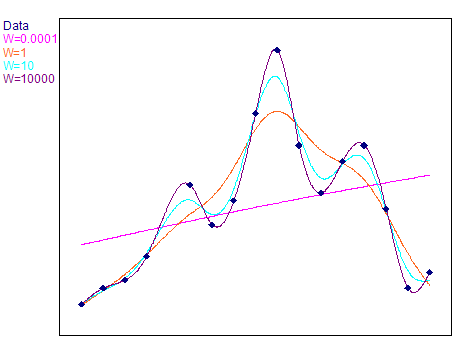
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
Compensatingspline({1, 2, 6, 9, 4, 7, 6, 4, 2}, 100, SPLINE_EQUIDISTANT, 0.0001) |
Interpoliert den Datensatz durch eine ausgleichende Spline-Kurve. Das Ergebnis ist eine Bestgerade mit 100 Punkten. |
Compensatingspline({1, 2, 6, 9, 4, 7, 6, 4, 2}, 100, SPLINE_EQUIDISTANT, 1000) |
Interpoliert den Datensatz durch eine ausgleichende Spline-Kurve. Das Ergebnis ist eine natürliche Spline-Kurve mit 100 Punkten. |
Siehe auch
Analyseobjekt Spline-Interpolation
Analyseobjekt Oberflächeninterpolation
Literatur
[1] "Carl de Boor": "A Practical Guide to Splines, Revised Edition". "Springer-Verlag, New York",2001.ISBN 0-387-95366-3.
