Hilbert (FPScript)
Berechnet die Hilbert-Transformation. Wird häufig verwendet zur Berechnung der Momentanamplitude oder Momentanfrequenz sowie zur Demodulation von Signalen.
Syntax
Hilbert(Signal [ , FFTLength = 0 ])
Die Syntax der Hilbert-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
|---|---|
Signal |
Der reelle Datensatz, von dem das analytische Signal berechnet werden soll. Der Datensatz sollte äquidistant abgetastet sein, da der Algorithmus die diskrete Fourier-Transformation (für äquidistante Daten) verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Ungültige Werte sind in diesem Argument nicht zulässig. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
FFTLength |
Die Länge der Fourier-Transformation welche zur Berechnung der Hilbert-Transformation benötigt wird. Die FFT-Länge muss größer gleich der Datenlänge sein. Wenn die angegebene FFT-Länge größer als die Datenlänge ist, dann werden Nullen für die interne Fourier-Transformation angehängt. Ein Wert von -1 setzt die FFT-Länge auf die nächst größere 2er-Potenz. Der Vorgabewert 0 setzt die FFT-Länge auf die Datenlänge. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich -1 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 0 gesetzt. |
Anmerkungen
Das Ergebnis hat die gleiche Struktur und Einheit wie das Argument Signal.
Bei zusammengesetzten Datenstrukturen wird nur die Y-Komponente verrechnet. Die X- bzw. Z-Komponenten werden, falls vorhanden, unverändert in das Ergebnis übernommen. Bei Datenmatrizen und Signalreihen erfolgt die Berechnung spaltenweise.
Die Hilbert-Transformation ist durch eine lineare Integraltransformation für ein (reell- oder komplexwertiges) Signal x(t) wie folgt definiert:
Mit dieser Definition lässt sich die Hilbert-Transformation in äquivalenter Form als Faltung ebenso schreiben als:
Durch Anwendung der Fourier-Transformation auf die letztgenannte Gleichung, berechnet sich die Übertragungsfunktion H der Hilbert-Transformation wie folgt als:
Mit anderen Worten: Die Hilbert-Transformation kann als eine Phasenverschiebung um -π/2 (d.h. -90 Grad) für positive Frequenzen und um π/2 (d.h. 90 Grad) für negative Frequenzen interpretiert werden. So ergibt beispielsweise die Hilbert-Transformation der Kosinusfunktion als Resultat die Sinusfunktion.
Als Referenz siehe [1] sowie [4].
Anwendung: Momentanamplitude, Momentanphase, Momentanfrequenz, Einhüllende sowie Demodulation von Signalen
Die Hilbert-Transformation wird häufig verwendet zur Berechnung von Momentangrößen des Originalsignals: der Momentanamplitude (Instantaneous Amplitude), Momentanphase (Instantaneous Phase) und Momentanfrequenz (Instantaneous Frequency). Die Momentanamplitude liefert außerdem die obere Einhüllende des zu analysierenden Signals.
Mithilfe dieser Momentangrößen lassen sich Signale zudem demodulieren (Amplitudendemodulation, Phasendemodulation und Frequenzdemodulation).
Die Berechnungen beziehen sich allerdings auf das aus der Hilbert-Transformation hergeleitete analytische Signal und nicht direkt auf die Hilbert-Transformation.
Details, Definitionen und Beispiele sind daher zu finden in der Online-Hilfe zur AnalyticSignal-Funktion oder zum Analyseobjekt Momentangröße.
Theoretischer Hintergrund: Algorithmus zur Berechnung der Hilbert-Transformation
Die oben angegebene zeitkontinuierliche Berechnungsvorschrift definiert die Übertragungsfunktion im Frequenzbereich. Der Algorithmus zur Berechnung der diskreten Hilbert-Transformation ist deshalb mit Hilfe der FFT und der diskreten Übertragungsfunktion H analog zum Algorithmus der AnalyticSignal-Funktion realisiert (vergleiche auch mit [1]):
Einziger Unterschied liegt in der Definition der Übertragungsfunktion.
Diese ist für gerade FFT-Längen nun gegeben als: H[k] = -i für k = 1, 2, ..., FFTLength/2 - 1 (entspricht den positiven Frequenzen) und H[k] = i für k = FFTLength/2 + 1, ..., FFTLength (entspricht den negativen Frequenzen). i bezeichnet hier die imaginäre Einheit. Sonderstellung nehmen die symmetrischen Koeffizienten k = 0 und k = FFTLength/2 ein. Für diese ist H[k] = 0.
Für ungerade FFT-Längen ist die Übertragungsfunktion analog gegeben als: H[k] = -i für k = 1, 2, ..., (FFTLength-1)/2 und H[k] = i für k = (FFTLength-1)/2 + 1, ..., FFTLength sowie außerdem H[0] = 0.
Der FPScript-Algorithmus zur Berechnung der diskreten Hilbert-Transformation entspricht also dem FPScript-Algorithmus der AnalyticSignal-Funktion mit Ausnahme der Definition der Übertragungsfunktion. Der analoge Code ist zu finden in der Online-Hilfe zur AnalyticSignal-Funktion.
Einfluss der FFT-Länge: Mittels Zero-Padding, d.h. durch Wahl der FFT-Länge größer als die Datenlänge, wird die Auflösung der für den Algorithmus benötigten FFT erhöht. DasBerechnungsresultat kann dadurch verbessert werden. Nachfolgendes Beispiel verdeutlicht dies.
Hinweis Ein reellwertiges Signal x(t) kann nun mittels der Hilbert-Transformation in ein komplexes Signal z(t) wie folgt transformiert werden:
Die Übertragungsfunktion dieser Transformation entspricht der Transformation aus der Definition der AnalyticSignal-Funktion. Die Hilbert-Transformation kann also äquivalent als Imaginärteil des zum Signal x(t) zugehörigen analytischen Signals definiert werden.
Verfügbarkeit
Option Spektralanalyse
Beispiele
Imag(AnalyticSignal(realSig))
Liefert die Hilbert-Transformation eines reellwertigen Signals. Der Code ist äquivalent zu Hilbert(realSig).
realSig + 1i * Hilbert(realSig)
Transformiert ein reellwertiges Signal in ein analytisches Signal, dessen Imaginärteil der Hilbert-Transformation entspricht. Der Code ist äquivalent zu AnalyticSignal(realSig).
Dim t = Series(0, 10, 0.005)
Hilbert(Signal(Cos(t), t))
Berechnet die Hilbert-Transformation der Kosinusfunktion. Als Ergebnis erhält man die Sinusfunktion.
Dim t = Series(-25, 25, 0.005)
Dim sig = Signal(Sinc(t), t)
Dim hilbTrafo = Hilbert(sig, NumberOfRows(sig))
List("Hilbert Trafo calculated", hilbTrafo, "Hilbert Trafo exact", Signal((1-Cos(t))/t, t))
Berechnet die Hilbert-Transformation der Sinc-Funktion. Es wird ebenso das exakte Resultat mit ausgegeben, welches durch die Funktion 1/t - Cos(t)/t gegeben ist. Der Vergleich in einem 2D-Diagramm liefert:
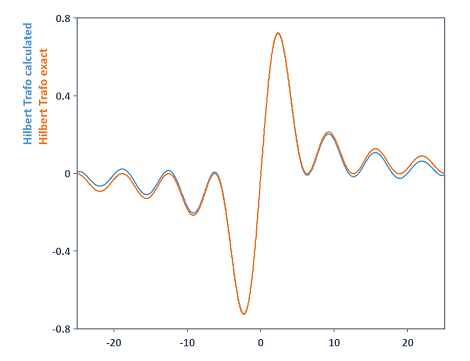
Erhöht man in diesem Beispiel die FFT-Länge bei der Berechnung der Variablen hilbTrafo beispielsweise auf den Wert 131072, so liefert dies in diesem Fall ein präziseres Berechnungsresultat für die Hilbert-Transformation. Beide Kurven stimmen jetzt nahezu überein:
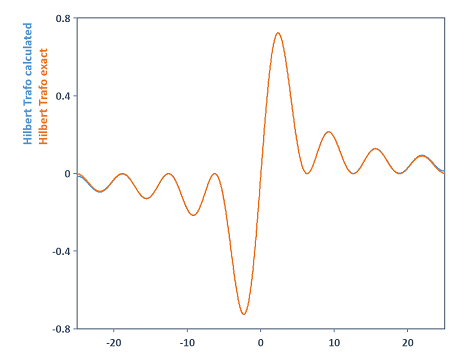
Siehe auch
Literatur
[1] S. Lawrence Marple, Jr.: Computing the Discrete-Time "Analytic" Signal via FFT. In: IEEE Transactions on Signal Processing, Vol. 47, No.9. http://ieeexplore.ieee.org/iel5/78/16975/00782222.pdf?arnumber=782222,1999.
[2] B. Boashash: Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals. In: Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538. 1992.
[3] Bernard Picinbono: On Instantaneous Amplitude and Phase of Signals. In: IEEE Trans. Signal Processing, Vol. 45, No. 3. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.178.833,1997.
[4] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck: Discrete-Time Signal Processing, 2nd Ed.. Upper Saddle River, NJ: Prentice Hall,1999.
