Derivative (FPScript)
Berechnet die erste Ableitung.
Syntax
Derivative(Signal [ , Mode = DERIVATIVE_CENTRAL_3_POINTS ])
oder
Derivative(Amplitude, Time [ , Mode = DERIVATIVE_CENTRAL_3_POINTS ])
Die Syntax der Derivative-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||
|---|---|---|---|---|---|---|---|
Signal |
Das Signal, dessen erste Ableitung berechnet wird. Wenn das Argument eine Datenreihe oder eine Datenmatrix ist, wird Eins als Schrittweite dX für die Ableitung angenommen. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||
Amplitude |
Die Y-Komponente des zu bearbeitenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
Time |
Die X-Komponente des zu bearbeitenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||
Mode |
Zur diskreten Approximation der Ableitung werden Finite-Differenzen in Form von zentralen Differenzenquotienten verwendet. Die Ordnung der verwendeten Finiten-Differenzen bestimmt die Genauigkeit zur numerischen Berechnung der Ableitung. Das Argument Mode kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert DERIVATIVE_CENTRAL_3_POINTS gesetzt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Die Einheit des Ergebnisses ist gleich dem Quotienten der Einheiten von Amplitude und Time bzw. der Y- und X-Komponente von Signal. Bei Datenmatrizen und Signalreihen erfolgt die Berechnung spaltenweise. Die Werte werden vor der Berechnung in 64-Bit Fließkommazahlen gewandelt. Die X- bzw. Z-Komponenten werden, falls vorhanden, unverändert in das Ergebnis übernommen. Die numerische Ableitung wird im Modus DERIVATIVE_CENTRAL_3_POINTS für äquidistant abgetastete Datensätze (Schrittweite dX) mit Hilfe des folgenden zentralen Differenzenquotienten berechnet (mindestens drei Datenpunkte vorausgesetzt):
Dieser Fall entspricht einer Mittelung der rechts- und linksseitigen einseitigen Differenzenquotienten, d.h.:
Im Modus DERIVATIVE_CENTRAL_5_POINTS wird die numerische Ableitung für äquidistant abgetastete Datensätze mit Hilfe des folgenden zentralen Differenzenquotienten berechnet (mindestens fünf Datenpunkte vorausgesetzt):
Für beide Varianten stehen an den Rändern nicht genügend Stützstellen für die Berechnung der zentralen Differenzen zur Verfügung. Dort wird die numerische Ableitung daher mittels Nicht-Zentraler-Finiter-Differenzenquotienten berechnet, welche die gleiche Ordnung besitzen. Die Berechnungsvorschriften an den Rändern sind in [1] angegeben.
Die angegeben Berechnungsvorschriften der numerischen Ableitung können ebenso für nicht-äquidistant abgetastete Datensätze verallgemeinert werden, siehe [1]. Diese Berechnungsvorschriften sind ebenso in FlexPro implementiert und werden automatisch verwendet, sobald der zugrundeliegende Datensatz eine nicht-äquidistante Abtastung besitzt.
Hinweis Generell gilt: Je höher die Ordnung bei Wahl der Finiten-Differenzen, desto größer ist die Genauigkeit bei Bestimmung der Ableitung für glatte (nicht-verrauschte) Datensätze. Sind die Datensätze hingegen verrauscht, so wird der numerische Fehler bei Bestimmung der Ableitung vergrößert, wenn eine höhere Ordnung bei Wahl der Finiten-Differenzen verwendet wird. Die Wahl des Ableitungsmodus sollte also auch von dem Rauschen / der Glätte des zugrundeliegenden Datensatzes abhängig gemacht werden. Der Modus DERIVATIVE_CENTRAL_5_POINTS ist beispielsweise für Crash-Auswertungen vorgeschrieben, siehe Richtlinien J1727 aus [2] und ECE-R94 aus [3].
Ist man hingegen am Frequenz-Spektrum interessiert, so hilft es die Ableitungsregeln als digitale Filter (siehe auch [4]) zu betrachten. Die Ableitungsregeln besitzen hierbei den folgenden Amplitudengang. Aufgezeichnet ist ebenso der ideale Differentiator (Filterverlauf der kontinuierlichen Differentiation) sowie die vorwärts-und rückwärts-gerichtete Differentiation mittels der Diff-Funktion:
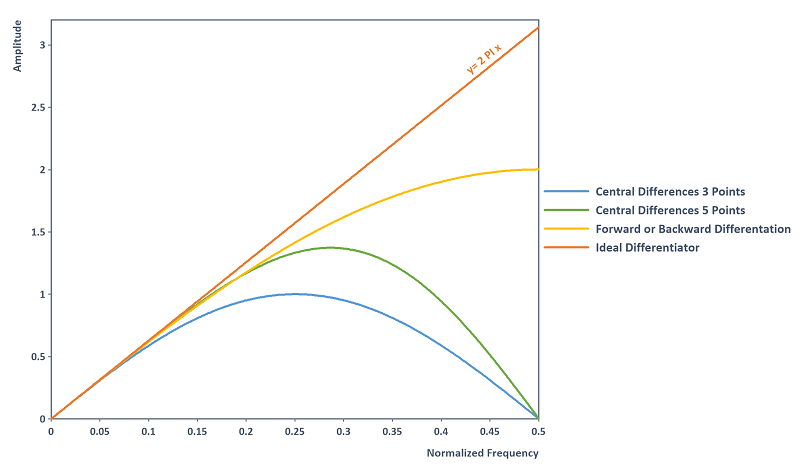
Beobachtung: Die zentrale 3-Punkte-Regel sowie die zentrale 5-Punkte-Regel unterdrücken hochfrequentes Rauschen im Bereich der Nyquist Grenze 0,5. Die zentrale-5-Punkte-Regel besitzt dabei im gesamten Frequenzbereich eine genauere Amplitudengang-Approximation des idealen Differentiators als die zentrale-3-Punkte-Regel. Die einseitigen vorwärts- und rückwärts-gerichteten Differenzenquotienten besitzen zwar ebenso eine präzisere Amplitudengang-Approximation des idealen Differentiators, verstärken dadurch aber hochfrequentes Rauschen. Es sei angemerkt, dass die zentralen Differenzenregeln einen konstanten Phasengang von 90 Grad besitzen und damit mit dem Phasengang des idealen Differentiators exakt übereinstimmen. Die vorwärts- und rückwärts-gerichteten Differenzenquotienten besitzen hingegen eine lineare Phasenverschiebung.
Verfügbarkeit
FlexPro View, Basic, Professional, Developer Suite
Beispiele
Derivative(Signal)
Berechnet die diskrete Ableitung eines beliebigen Signals mit Hilfe der zentralen 3-Punkte-Regel.
Derivative({1.0, 3.0, 5.0, 5.0, 4.0, 3.0})
Berechnet die Ableitung {2, 2, 1, -0.5, -1, -1} der als Argument angegebenen Datenreihe, wobei 1.0 als Schrittweite dX angenommen wird. Das Ergebnis besitzt die gleiche Datensatzlänge wie der Eingangsdatensatz.
Diff({1.0, 3.0, 5.0, 5.0, 4.0, 3.0}, DIFF_QUOTIENT_FORWARD)
Berechnet die Differenzenquotienten benachbarter Werte mittels der Diff-Funktion und liefert {2, 2, 0, -1, -1} als Ergebnis. Die Diff-Funktion verwendet also Nicht-Zentrale-Finite-Differenzen (von erster Ordnung). Die Datensatzlänge des Ergebnisses wird gegenüber dem Eingangsdatensatz um Eins reduziert.
Dim x = Series(-6, 6, 0.5)
Derivative(Signal(2.2 + 6.1*x + 3.6*x^2 + 12*x^3 - x^4, x), DERIVATIVE_CENTRAL_5_POINTS)
Berechnet die Ableitung eines Polynoms vierten Grades an den Stützstellen x. Das Ergebnis stimmt mit der exakten Ableitung Signal(6.1 + 7.2*x + 36*x^2 - 4*x^3, x) überein.
Dim x = Series(-3, 3, 0.1)
Dim f = Signal(Sin(x^2), x)
Dim derivExact = Signal(2*x*Cos(x^2), x)[[ 1.0 ]]
Absolute(Derivative(f, DERIVATIVE_CENTRAL_3_POINTS)[[ 1.0 ]] - derivExact)
Ermittelt für den Modus DERIVATIVE_CENTRAL_3_POINTS den Fehler bei Berechnung der numerischen Ableitung der glatten Funktion f = Sin(x2) an der Stelle 1.0. Der Fehler ist proportional zu 0.01. Wählt man hingegen DERIVATIVE_CENTRAL_5_POINTS, so liefert dies höhere Genauigkeit mit einem Fehler proportional zu 0.0001. Verwendet man stattdessen die Diff-Funktion, so wird die Ableitung mit einem Fehler proportional zu 0.1 berechnet (kleinste Genauigkeit). Zur Approximation der Ableitung sollte also in der Regel die Derivative-Funktion der Diff-Funktion vorgezogen werden.
Siehe auch
SavitzkyGolayDerivative-Funktion
Literatur
[1] Bengt Fornberg: Generation of Finite Difference Formulas on Arbitrarily Spaced Grids. In: Mathematics of Computation, Vol. 51, No. 184, Pages 699-706. https://doi.org/10.1090/S0025-5718-1988-0935077-0,1988.
[2] Safety Test Instrumentation Stds Comm: Calculation Guidelines for Impact Testing (J1727). In: SAE International. http://standards.sae.org/j1727_201502/,2015.
[3] UN Vehicle Regulations: Regulation No. 94 - Frontal collision protection (ECE-R94). In: Concerning the Adoption of Uniform Technical Prescriptions for Wheeled Vehicles, Equipment and Parts which can be Fitted and/or be Used on Wheeled Vehicles and the Conditions for Reciprocal Recognition of Approvals Granted on the Basis of these Prescriptions. http://www.unece.org/trans/main/wp29/wp29regs81-100.html,2013.
[4] Tilman Butz: Fourier Transformation for Pedestrians. Springer Berlin Heidelberg New York,http://www.springer.com/de/book/9783319169842,2015.ISBN 3-540-23165-X.
